Inverse Trigonometric Functions – IA Report
Unit: Inverse Trigonometric Functions
Topic: A Graphical & Real-life Exploration using Technology
Student: AKHIL KUMAR MEENA
Class: XII - C
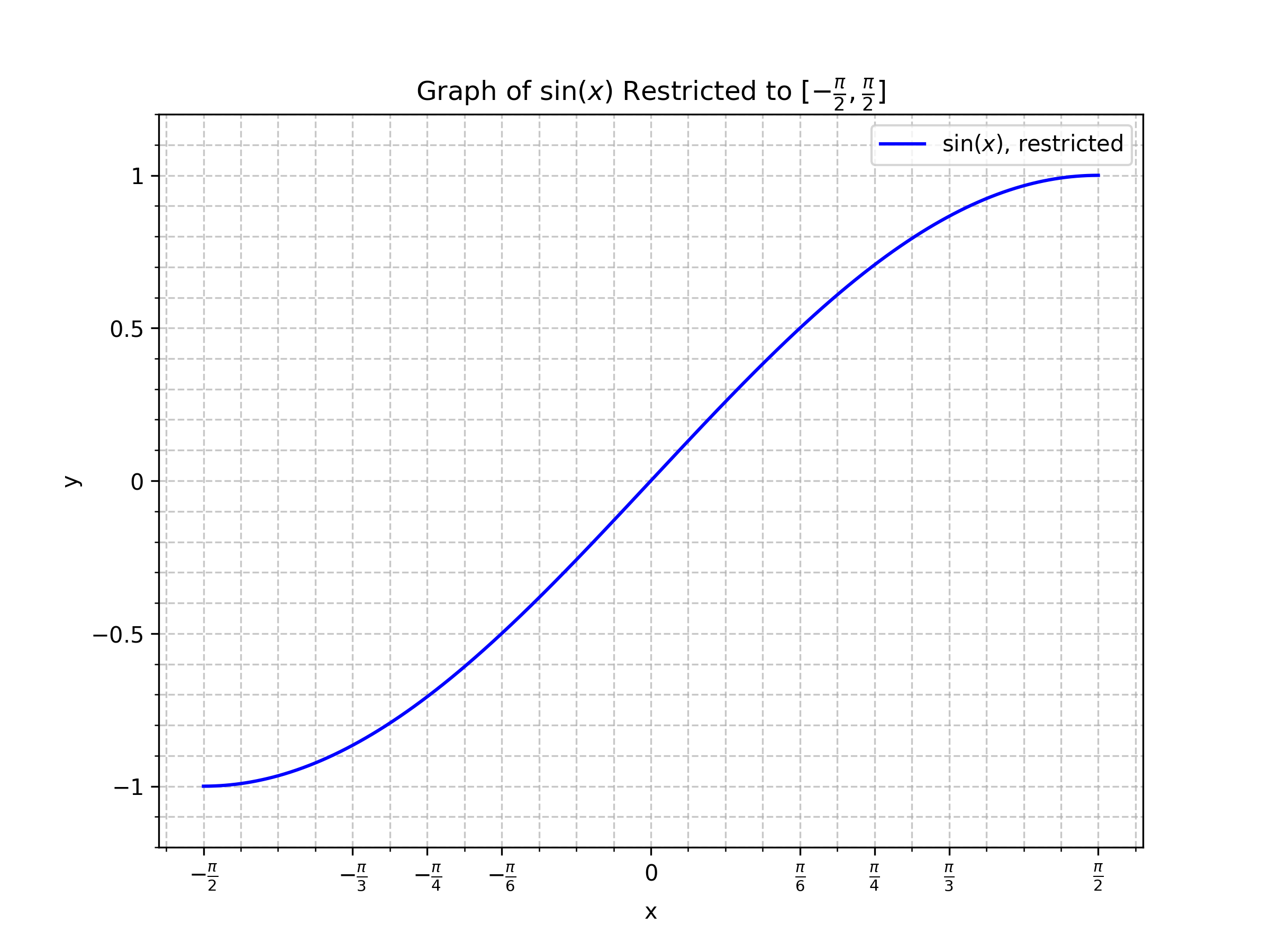
For Sine Function
Domain and Range of sin(x)
y = sin(x)
- Domain: (-∞, ∞)
- Range: [-1, 1]
Sine is periodic and repeats its values infinitely, so it is not one–one. Hence, its inverse cannot exist on the full domain.
To make it invertible, we restrict the domain to [-π/2, π/2]. On this interval, sine is strictly increasing and one–one.
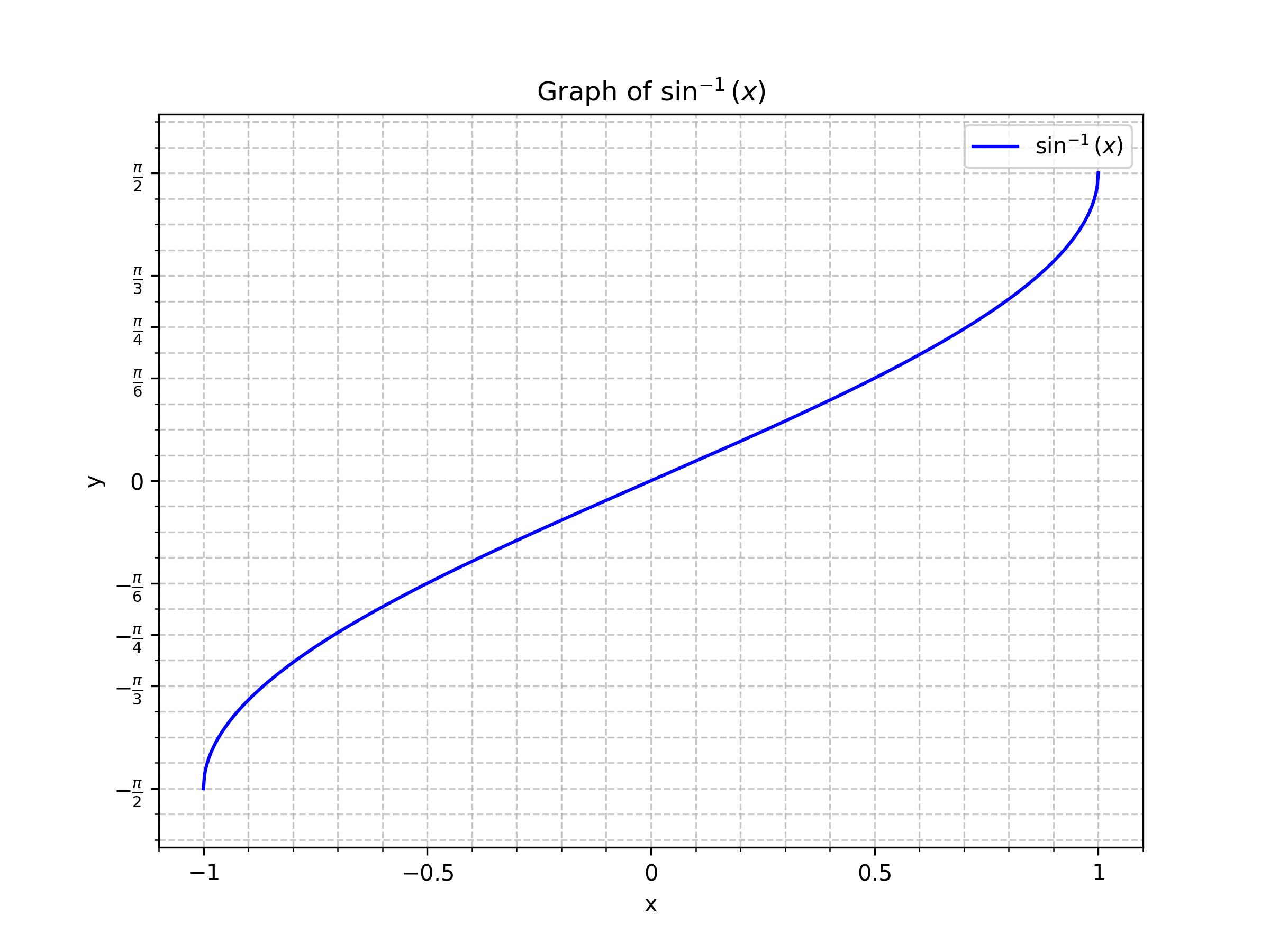
Inverse Definition: y = sin-1(x)
- Domain: [-1, 1]
- Range: [-π/2, π/2]
Graphs of Sine and Inverse Sine
For Cosine Function
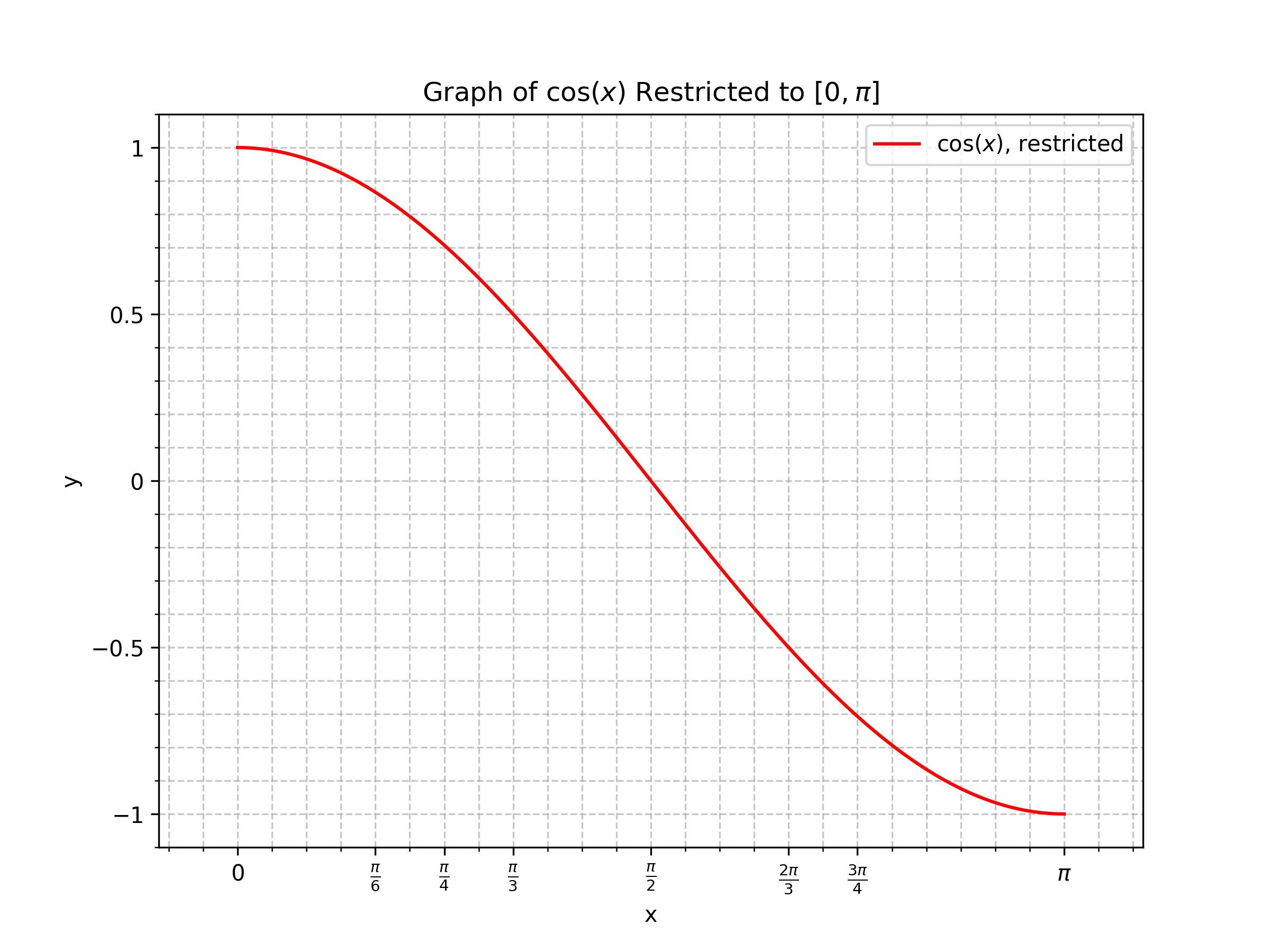
Domain and Range of cos(x)
y = cos(x)
- Domain: (-∞, ∞)
- Range: [-1, 1]
Cosine is periodic and repeats values, so it is not one–one. Hence, its inverse cannot exist on the full domain.
To make it invertible, we restrict the domain to [0, π]. On this interval, cosine is strictly decreasing and one–one.
Inverse Definition: y = cos-1(x)
- Domain: [-1, 1]
- Range: [0, π]
Graphs of Cosine and Inverse Cosine

Deriving the Identity
We want to prove: sin-1(x) + cos-1(x) = π/2
Let θ = sin-1(x). Then sin θ = x, with θ ∈ [-π/2, π/2].
Now, cos(π/2 - θ) = sin θ = x
Therefore, cos-1(x) = π/2 - θ = π/2 - sin-1(x)
Hence proved.
Verification Table
| x | sin-1(x) (rad) | cos-1(x) (rad) | Sum (rad) | π/2 (rad) |
|---|---|---|---|---|
| -0.8 | -0.927295 | 2.498092 | 1.570796 | 1.570796 |
| 0.0 | 0.000000 | 1.570796 | 1.570796 | 1.570796 |
| 0.6 | 0.643501 | 0.927295 | 1.570796 | 1.570796 |
Conclusion
- We restricted domains of sine and cosine to make them invertible.
- sin(x) restricted to [-π/2, π/2] → inverse sin-1(x)
- cos(x) restricted to [0, π] → inverse cos-1(x)
- Identity sin-1(x) + cos-1(x) = π/2 was derived and verified.
- Graphs make the restrictions and ranges clear.
- Applications: navigation, physics, engineering.